Sākotnējais fails ‎(3 000 × 3 000 pikseļi, faila izmērs: 2,15 MB, MIME tips: image/jpeg)

Fails ir no Wikimedia Commons, tāpēc tas var tikt izmantots citos projektos. Apraksts ir faila apraksta lapā, kas ir parādīta zemāk.

This image was uploaded in the JPEG format even though it consists of non-photographic data. This information could be stored more efficiently or accurately in the PNG or SVG format. If possible, please upload a PNG or SVG version of this image without compression artifacts, derived from a non-JPEG source (or with existing artifacts removed). After doing so, please tag the JPEG version with {{Superseded|NewImage.ext}} and remove this tag. This tag should not be applied to photographs or scans. If this image is a diagram or other image suitable for vectorisation, please tag this image with {{Convert to SVG}} instead of {{BadJPEG}}. If not suitable for vectorisation, use {{Convert to PNG}}. For more information, see {{BadJPEG}}.

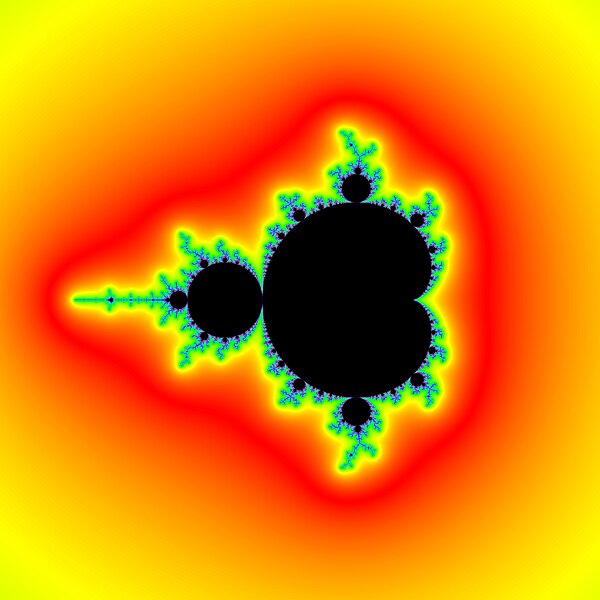
Apraksts

Mandelbrot set for F(z) = z² + c using Milnor algorithm = DEM/M

Avots

Paša darbs

Autors

Adam majewski

Atļauja:
(Šī faila izmantošana citur)

This work has been released into the public domain by its author, Adam majewski at angļu Vikipēdija. This applies worldwide.
In some countries this may not be legally possible; if so:
Adam majewski grants anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

Compare with

Image with C++ code, without zoom and different algorithm
contiunous escape time with C code
continous colour but without algorithm

Kopsavilkums

The image contains a rectangular region: corners of c-plane C_Plane.eCxMin:= -2,5 C_Plane.eCxMax:= 1,5 C_Plane.eCyMin:= -2 C_Plane.eCyMax:= 2

center and sides of c-plane C_Plane.Center.x:= -0,5 C_Plane.Center.y:= 0 C_Plane.width:= 4 C_Plane.height:= 4

Bitmap size in pixels: Bitmap Width= 3000 Bitmap Height= 3000

Number of bitmap points = 9000000 points

Drawing Time := 21625 miliseconds

Bitmapa.PixelFormat = pf32bit Maximal number of iterations= 1000

Escape Radius= 100

Image is made with program MandelbrotSetExplorer archive copy at the Wayback Machine It is made using: programing language: object Pascal IDE: Borland Delphi 6.0 - 7.0 personal edition - 10.0 Turbo Explorer programing style : libaries : standard = VCL

OS: windows

Bitmap image is transformed to jpg with IrfanView

author: Adam Majewski fraktal.republika.pl 20003- 2007

Delphi Pascal src code

{
spoken language: english
programming language: Pascal ( Borland object Pascal )
compiler: VER 140
IDE: Borland Delphi 7.0 personal edition
programming style : obiektowy
programming method : visual (RAD)
target: CPU
library: standard =  VCL
program type : GUI application
licence: GNU GPL
OS: win32 (windows 98 SE
hardware: PC
platform:  ix86
author: Adam Majewski
adammaj1- at - o2 - dot - pl
republika.pl/fraktal
walbrzych
poland
2005.12.12
}

Computing color from RGB gradient

 // **********************************************************************************************************
    function Rainbow(iMin, iMax, i: Integer): TColor;
 // gives rainbow gradient of color

 // Opracował Witold J.Janik; WJJ@CAD.PL
// ***
// Funkcja FnTecza umożliwia narysowanie
// tęczy przy zmianie [i] od [iMin] do [iMax]
// podziękowania dla Andrzeja Wšsika z [pl.comp.lang.delphi]
//  http://4programmers.net/view.php?id=201
var
  m: Double;
  r, g, b, mt: Byte;
begin
  m := (i - iMin)/(iMax - iMin + 1) * 6;
  mt := abs((round(frac(m)*$FF)));// added abs ; why ? erange check eror
  case Trunc(m) of
  0: begin
      R := $FF;
      G := mt;
      B := 0;
    end;
  1: begin
      R := $FF - mt;
      G := $FF;
      B := 0;
    end;
  2: begin
      R := 0;
      G := $FF;
      B := mt;
    end;
  3: begin
      R := 0;
      G := $FF - mt;
      B := $FF;
    end;
  4: begin
      R := mt;
      G := 0;
      B := $FF;
    end;
  5: begin
      R := $ff;
      G := 0;
      B := $FF - mt;
    end;
end; // case

  Result := rgb(R,G,B);
end;
//-------------------------------

exterior Distance Estimastion Method for Mandelbrot set (DEM/M)

Function PointIsInCardioid (Cx,Cy:extended):boolean;
 //Hugh Allen
 // http://homepages.borland.com/ccalvert/Contest/MarchContest/Fractal/Source/HughAllen.zip
  var DeltaX,DeltaY:extended;
      //
      PDeltyX,PDeltyY:extended;
      //
      ZFixedX,ZFixedY:extended;

  begin
     result:=false;
     // cardioid checkig - thx to Hugh Allen
     //sprawdzamy Czy punkt  C jest w głównej kardioidzie
     //Cardioid in squere :[-0.75,0.4] x [ -0.65,0.65]
     if InRange(Cx,-0.75,0.4)and InRange(Cy,-0.65,065) then
      begin
        // M1= all C for which Fc(z) has  attractive( = stable) fixed point
        // znajdyjemy punkt staly z: z=z*z+c
        // czyli rozwiazujemy rownanie kwadratowe
        // zmiennej zespolonej o wspolczynnikach zespolonych
        // Z*Z - Z + C = 0
        //Delta:=1-4*a*c; Delta i C sa liczbami zespolonymi
        DeltaX:=1-4*Cx;
        DeltaY:=-4*Cy;
        // Pierwiastek zespolony z delty
        CmplxSqrt(DeltaX,DeltaY,PDeltyX,PDeltyY);
        // obliczmy punkt staly jeden z dwóch, ten jest prawdopodobnie przycišgajšcy
        ZFixedX:=1.0-PDeltyX; //0.5-0.5*PDeltyX;
        ZFixedY:=PDeltyY; //-0.5*PDeltyY;
        // jesli punkt stały jest przycišgajšcy
        // to należy do M1
        If (ZfixedX*ZFixedX + ZFixedY*ZFixedY)<1.0
          then result:=true;

         
          // ominięcie iteracji M1 przyspiesza 3500 do 1500 msek
        end; // if InRange(Cx ...

  end;
//------------------------------------
Function PointIsInComponent (Cx,Cy:extended):boolean;
//Hugh Allen
// http://homepages.borland.com/ccalvert/Contest/MarchContest/Fractal/Source/HughAllen.zip

  var Dx:extended;
  begin
    result:=false;
    // czy punkt C nalezy do koła na lewo od kardioidy
    // circle: center = -1.0  and radius 1/4
    dx:=Cx+1.0;
    if (Dx*Dx+Cy*Cy) < 0.0625
      then result:=true;

  end;
Function GiveDistance(xy2,eDx,eDy:extended):extended;

begin
    result:=2*log2(sqrt(xy2))*sqrt(xy2)/sqrt(sqr(eDx)+sqr(eDy));
  end;

//------------------------------------

//------------------------------
Procedure DrawDEM_DazibaoTrueColor; 
// draws Mandelbrot set in black and its complement in true color
// see   http://ibiblio.org/e-notes/MSet/DEstim.htm
// by  Evgeny Demidov
//
// see also
//http://www.mandelbrot-dazibao.com/Mset/Mset.htm
// translation ( with modification) of Q-Basic program:
//  http://www.mandelbrot-dazibao.com/Mset/Mdb3.bas
//
// see also my page http://republika.pl/fraktal/mset_dem.html

var iter:integer;
     iY,iX:integer;
     eCy ,eCx:extended; // C:=eCx + eCy*i
     eX,eY:extended;    // Zn:=eX+eY*i
     eTempX,eTempY:extended;
     eX2,eY2:extended;  //x2:=eX*eX;  y2:=eY*eY;
     eXY2:extended;  //  xy2:=x2+y2;
     eXY4:extended;
     eTempDx,eTempDy:extended;
     eDx,eDy:extended; // derivative
     distance:extended;
     color:TColor;

begin
  //compute bitmap
  for iY:= iYmin to iYMax do
    begin
      eCy:=Convert_iY_to_eY(iY);
      for iX:= iXmin to iXmax do
        begin
          eCx:=Convert_iX_to_eX(iX);
          If not PointIsInCardioid (eCx,eCy) and not PointIsInComponent(eCx,eCy)
            then
              begin
                //  Z0:=0+0*i
                eX:=0;
                eY:=0;
                eTempX:=0;
                eTempY:=0;
                //
                eX2:=0;
                eY2:=0;
                eXY2:=0;
                //
                eDx:=0;
                eDy:=0;
                eTempDx:=0;
                eTempDy:=0;
                //
                iter:=0;
                // iteration of Z ; Z= Z*z +c
                while ((iter<IterationMax) and (eXY2<=BailOut2)) do
                  begin
                    inc(iter);
                    //
                    eTempY:=2*eX*eY + eCy;
                    eTempX:=eX2-eY2 + eCx;
                    //
                    eX2:=eTempX*eTempX;
                    eY2:=eTempY*eTempY;
                    //
                    eTempDx:=1+2*(eX*eDx-eY*eDy);
                    eTempDy:=2*(eX*eDY+eY*eDx);
                    //
                    eXY2:=eX2+eY2;
                    //
                    eX:=ETempX;
                    eY:=eTempY;
                    //
                    eDx:=eTempDx;
                    eDy:=eTempDy;
                  end; // while

                // drawing procedure
                if (iter<IterationMax)
                then
                  begin
                    distance:= GiveDistance(eXY2,eDx,eDy);
                    color:=Rainbow(1,500,Abs(Round(100*Log10(distance)) mod 500));
                    with Bitmap1.FirstLine[iY*Bitmap1.LineLength+iX] do
                        begin
                          B := GetBValue(color);
                          G := GetGValue(color);
                          R := GetRValue(color);
                          //A := 0;
                        end; // with FirstLine[Y*LineLength+X]

                end // if (iter<IterationMax) then
              else  with Bitmap1.FirstLine[iY*Bitmap1.LineLength+iX] do
                        begin
                          B := 0;
                          G := 0;
                          R := 0;
                          //A := 0;
                        end;
             //--- end of drawing procedure ---
            end //  If not PointIsInCardioid ... then
          else with Bitmap1.FirstLine[iY*Bitmap1.LineLength+iX] do
                        begin
                          B := 0;
                          G := 0;
                          R := 0;
                          //A := 0;
                        end;
         //--- If not PointIsInCardioid ...
        end; // for iX
      end; // for iY

end;
//------------------------------------------------------

Bitmap

Interface

  uses graphics;

  CONST
  PixelCountMax = 32768;

  TYPE
  //http://www.efg2.com/Lab/ImageProcessing/Scanline.htm
  // 24-bit color bitmap
   TRGBTriple =RECORD
                rgbtBlue : BYTE;
                rgbtGreen: BYTE;
                rgbtRed  : BYTE;
              END;
  TRGBTripleArray = ARRAY[0..PixelCountMax-1] OF TRGBTriple;
  pRGBTripleArray = ^TRGBTripleArray;
  //
  TRGB32 = record B, G, R, A: Byte; end;
  TRGB32Array = array[0..MaxInt div SizeOf(TRGB32)-1] of TRGB32;
  PRGB32Array = ^TRGB32Array;

  //-----------------------

  TBitmap32bit=class(TBitmap)
        public
          LineLength : Longint;
          FirstLine  : PRGB32Array;
          Procedure Default;
          Procedure Clear;
          Procedure Refresh;

    end; // class
 //--------------------------

 Var  Bitmap1:TBitmap32bit;
      iXmin,iYmin,iXmax,iYmax  :integer;
      // pf24bit
      LineLength24 : Longint;
      FirstLine24  : pRGBTripleArray;
      Row24   :  pRGBTripleArray;
//----------------------------------------------------
Implementation
//----------------------------------------------------

Procedure TBitmap32bit.Default;

  begin

    Bitmap1.Width:=400; //
    Bitmap1.Height:=400; //
    //
    Bitmap1.Refresh;

    
  end;
//------------------------------------------

 Procedure TBitmap32bit.Clear;
   // clear (= make white)  all points of the Bitmap1
  var iX,iY:integer;
  begin

    for iX:=0 to Bitmap1.Width-1 do
      For iY :=0 to Bitmap1.Height-1 do
         with Bitmap1.FirstLine[iY*Bitmap1.LineLength+iX] do
                  begin // all points white
                    B := 255;
                    G := 255;
                    R := 255;
                    //A := 0;
                  end;
  end;
//---------------------------------------------------------------
Procedure TBitmap32bit.Refresh;
begin
    iXmin:=0;
    iYmin:=0;
    iXmax:=Bitmap1.Width-1;
    iYmax:=Bitmap1.Height-1;
    //
    Bitmap1.FirstLine := Bitmap1.Scanline[0];
    Bitmap1.LineLength := (Longint(Bitmap1.Scanline[1]) - Longint(Bitmap1.FirstLine)) div SizeOf(TRGB32);
    //
end;
//---------------------------------------------

Initialization
Bitmap1 := TBitmap32bit.Create;	{ construct the Bitmap1 object }
//
Bitmap1.PixelFormat:=pf32bit;
//
Bitmap1.Default; // see BitmapU
//---------------------------------------
END.

Faila hronoloģija

Uzklikšķini uz datums/laiks kolonnā esošās saites, lai apskatītos, kā šis fails izskatījās tad.

	Datums/Laiks	Attēls	Izmēri	Dalībnieks	Komentārs
tagadējais	2007. gada 27. aprīlis, plkst. 14.57		3 000 × 3 000 (2,15 MB)	wikimediacommons>Soul windsurfer	{{Information \|Description=Mandelbrot set for F(z)=z*z+c using Milnor algorithm = DEM/M \|Source=self-made \|Date= \|Author= User:Adam majewski {{PD-user-en\|Adam majewski}} }}

Faila lietojums

Šo failu izmanto šajā 1 lapā:

Mandelbrota kopa

Attēls:Demm 2000 Mandelbrot set.jpg

Satura rādītājs

Compare with

Kopsavilkums

Delphi Pascal src code

Computing color from RGB gradient

exterior Distance Estimastion Method for Mandelbrot set (DEM/M)

Bitmap

Captions

Šajā failā attēlotais

attēlo

izveidotājs

Šai īpašībai ir vērtība, bet tā ir nezināma

autortiesību statuss

copyrighted, dedicated to the public domain by copyright holder ^angļu

licence

released into the public domain by the copyright holder ^angļu

faila avots

augšupielādētāja oriģināldarbs

medija veids

image/jpeg

Faila hronoloģija

Faila lietojums

Navigācijas izvēlne

Attēls:Demm 2000 Mandelbrot set.jpg

Compare with

Kopsavilkums

Delphi Pascal src code

Computing color from RGB gradient

exterior Distance Estimastion Method for Mandelbrot set (DEM/M)

Bitmap

Captions

Šajā failā attēlotais

attēlo

izveidotājs

Šai īpašībai ir vērtība, bet tā ir nezināma

autortiesību statuss

copyrighted, dedicated to the public domain by copyright holder angļu

licence

released into the public domain by the copyright holder angļu

faila avots

augšupielādētāja oriģināldarbs

medija veids

image/jpeg

Faila hronoloģija

Faila lietojums

Navigācijas izvēlne

Meklēt

copyrighted, dedicated to the public domain by copyright holder ^angļu

released into the public domain by the copyright holder ^angļu